¿Es posible, utilizando tan
sólo la regla y compás, constuir un cuadrado que tenga
exactamente la misma área que
un circulo dado ?
Respuesta:(no y 1000 veces no!)
Aunque ya se ha demostrado que esta
construción exacta es imposible
podemos encontrar construciones de
aproximaciones muy interesantes.
Legiones de grandes matemáticos
y aficionados se han dedicado a buscar
demostraciones gráficas aproximadas
de p.
Estas demostraciones son encantadoras,
y lejos de intentar demostrar
que podriamos llegar a "la
cuadratura exacta del circulo" sirven para afinar el
ingenio en la geometira.
Esta página siempre he querido
realizarla pero no me he atrevido a montarla
pero, gracias al empuje de unos grandes
colaboradores que dominan la
cuadratura del circulo infinitamente más que yo.
Abelardo
Falletti /Rosario - Argentina
(1999)
SIGNIFICADO DE LA CUADRATURA
DEL CIRCULO
Por Capitulos 1,
2, 3, 4,
5, 6.
 
|
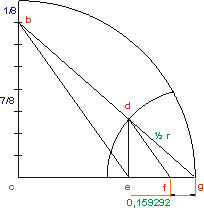
Tsu Ch'ung-Chin
Famoso astronomo chino en el siglo V Se dibuja un cuadrante de radio unidad, de modo que bc sea 7/8 del radio, dg sea 1/2 del radio, de sea paralela a ac y df sea paralela a be. Se demuestra fácilmente que la distancia fg es igual a 16/113, o sea, 0,1415929... Como 355/113 es igual a 3 + 16/113, si se dibuja un segmento igual al triple del radio y se le suma el segmento fg, el segmento resultante difiere de pi en menos de una millonesima de unidad. |
  |
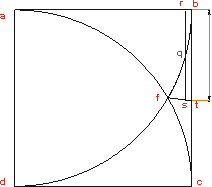
Thomas Hobbes
Famoso filósofo inglés Publicación "De corpore" 1655 en latín En un cuadrado de lado unidad se trazan ls arcos ac y bd, que son cuadrantes de sendas circunferencias de radio también unidad. Se biseca el arco bf; llamaremos q a su punto medio. Se traza ahora la recta rq, paralela al lado del cuadrado, y se prolonga hasta que qs sea igual a rq. Se dibuja ahora la recta fs, que corta al lado del cuadrado en t. Hobes mantenia que la longitud del arco bf es exactamente igual a la del segmento bt. Dado que la circunferencia contiene doce veces el arco bf, pi sería seis veces la longitud del segmento bt. De esta manera, el valor de pi resultaria ser 3,1419... |
Página en lentisima construcción