La cuadratura del círculo tiene un significado directamente
relacionado con las leyes de la Naturaleza y como consecuencia de ello
con el Hombre Integro, es decir cuerpo-psicología.
Por tal causa un círculo puede ser cuadrado matemática
y geométricamente mediante la proporción áurea (reproducción
desí mismo, como eje de la continuidad en la Naturaleza) y un Pi
de ocho dígitos porque el cerebro humano crea formas en base a una
ley de octavas.
La demostración correspondiente a la reproducción de
sí mismo dentro de la Unitotalidad Orgánica que es la Naturaleza,
que en tal caso de manifiesta como una Unidad, se basa en la ya conocida
División Aurea. Esta División Aurea es una unidad geométrica-matemática
que de un modo excepcional ha sido capturada como expresión realizada
por la mente-cerebro para manifestar su propio funcionamiento de auto-proyección.
Dicha unidad geométrica-matemática de reproducción
por unión de mitades es algo triangular y se expresa del siguiente
modo:

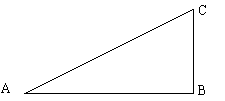
Este triángulo cumple con las proporciones requeridas para tener
en él la posibilidad de determinar una proporción áurea
y que indican que uno de los catetos debe medir la mitad del otro.
Así, en el ejemplo AB mide 6 cm y BC 3 cm. Pero para obtener
los valores unitarios de la proporción áurea se reducirán
esas medidas del siguiente modo:
AB = 1
BC = 0,5
Es decir la Unidad y su mitad exacta.
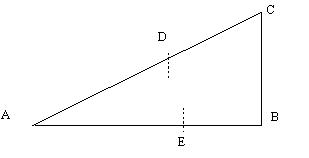
El procedimiento a continuación radica en cortar la hipotenusa
desde el punto C con la medida del cateto menor BC. Ese punto del
corte tendrá la letra D.
Luego se traslada la medida AD al cateto mayor AB cortándolo
en el punto E :
Para obtener el valor de la hipotenusa se utiliza el Teorema de Pitágoras:
= 1,118033989... (Valor de la hipotenusa)
Como consecuencia de ello la recta AD tiene el siguiente valor:
1,118033989... - 0,5 (valor a BC) = 0,618033989...
Y al bajar esa medida al cateto mayor éste queda dividido en dos fragmentos cuyos valores son:
0,618033989...
0,381966011...
Y cuya suma es naturalmente 1 (uno), la medida de la recta AB.
La característica de estos dos números irracionales es
la reproducción a través del cuadrado como potencia o radicalización:
A) el cuadrado de 0,618033988... es igual a 0,381966011...
B) la raíz cuadrada de 0,381966011... es igual a 0,618033988...
C) 0,6180033988... dividido 0,381966011... es igual a 1,618033988...
D) el cuadrado de 1,618033988... es igual a 2,618033988...
Eso en cuanto al aspecto matemático. Pero también ocurre
lo mismo en el territorio de la geometría.
El ejemplo muestra un rectángulo cuyos lados guardan la proporción
áurea ya descripta:
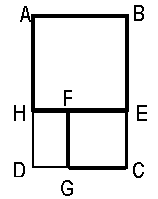
En el rectángulo original ABCD la relación áurea es la siguiente:
El cuadrado ABHE reproduce el rectángulo original en el rectángulo
HECD. El cuadrado FECG reproduce el rectángulo original en el rectángulo
HFGD, y así sucesivamente hacia arriba y hacia abajo.
Es decir que geométricamente este rectángulo se reproduce
a sí mismo tanto hacia lo más chico como hacia lo más
grande, tanto hacia arriba como hacia abajo. “Arriba” y “Abajo” implica
a la Unidad reproduciéndose a sí misma proyectada en
todas partes y en cada cosa.
Desde la antigüedad, cuando se planteó el problema de la
cuadratura del círculo, conocían -como es obvio- la solución
del mismo. Esto no es una idea, sino un hecho que queda demostrado en el
juego del ajedrez cuyo origen es realmente desconocido.
En dicho juego, el movimiento del caballo es un triángulo áureo
tal como se muestraen el gráfico siguiente:
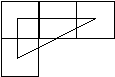
Las piezas en el juego de ajedrez se ubican en el centro de la casilla
y tomando las medidas de centro a centro queda configurado el triángulo
áureo en que un cateto mide 2 y el otro 1, que son las medidas que
exige la proporción áurea.
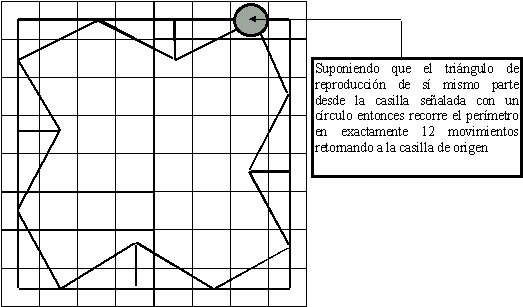
Lo notable es que el tablero de ajedrez es un cuadrado de ocho casillas
por lado, y este movimiento del triángulo áureo o de reproducción
de sí mismo recorre el perímetro de un modo circular recurrente
en 12 pasos o movimientos tal como se muestra a continuación:
la antigüedad y en la actualidad un matemático es
un sabio, no un especialista.
( Tomado de “Teoremas de la existencia humana”, de Abelardo
Falletti, edición 1999, ISBN 987-043-0217-8 )
volver