Encontrar en la serie de decimales de Pi un sistema recurrente en la estructura de los mismos ha sido y es el sueño de todo investigador en este tema.

Para comenzar en esa indagación hay que regresar al Capítulo 1, de esta serie de comentarios. Allí se expuso al finalizar dicho capítulo el siguiente gráfico:
 
 

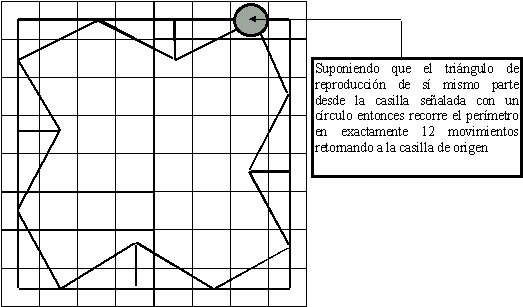
Este es el recorrido circular y recurrente del triángulo aúreo o de reproducción de sí mismo utilizando el perímetro del cuadrado de 8.

Este perímetro consta de 28 casillas, y el recorrido del mismo por parte del triángulo áureo constituye un cuadrado de 7 dentro del cuadrado de 8.

Este número 7 tiene una relación directa con el círculo recurrente cuando se lo relaciona con los demás números que van del 1 al 9:

1 / 7 = 0,142857 142857 ...

2 / 7 = 0,285714 285714 ...

3 / 7 = 0,428571 428571 ...

4 / 7 = 0,571428 571428 ...

5 / 7 = 0,714285 714285 ...

6 / 7 = 0,857142 857142 ...

8 / 7 = 1,142857 142857 ...

9 / 7 = 1,285714 285714 ...

Como puede observarse existe un círculo numérico giratorio recurrente constituido por seis números 142857, en los que faltan el número 3 y sus múltiplos 6 y 9.

El primer resultado obvio que surge de esta indagación es fragmentar los decimales de Pi de siete en siete:

Suma de guarismos

Ahora puede observarse que el primer fragmento de 7 decimales suma 28, es decir que es coincidente con el gráfico del cuadrado de 8 con el recorrido circular recurrente del triángulo áureo utilizando 28 casillas y constituyendo un cuadrado de 7 dentro del mismo.

Este primer fragmento con suma 28 ( cuatro lados de 7 del cuadrado interior ) se constituye en la clave que será el eje de la recurrencia circular y giratoria en los decimales de Pi, sea cual sea la cantidad de decimales que se obtengan. El segundo fragmento suma 46 y puesto en relación con la clave 28:

46 / 28 = 1,64 285714 285714 ... (recurrencia giratoria)

Lo notable radica en los tres primeros números de la serie, es decir 164, que son ajenos a la recurrencia, tienen la siguiente relación con los números faltantes en la recurrencia 142857, es decir 369:

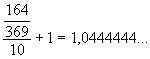
Este resultado es la medida de la recta que resuelve la cuadratura del círculo con un Pi de 7 decimales pertenecientes a este primer fragmento.

Prosiguiendo con los demás fragmentos de los decimales, el tercero es nuevamente 28, es decir es uno y el mismo que la clave del sistema de recurrencia.

El cuarto fragmento suma 29:

29 / 28 = 1,03 571428 571428 ... (recurrencia giratoria)

El quinto fragmento suma 39:

39 / 28 = 1,29 285714 185714 ... (recurrencia giratoria)

Y así sucesivamente hasta donde se obtengan decimales.

A quien le interese verificarlo en los hechos puede crear un programa para instalarlo en la computadora. Para ello deberá tener previsto lo siguiente:

a) todas las sumas de guarismos que arrojen cifras que no son múltiplos de 7, funcionan a la perfección con los ejemplos anteriores.

b) las sumas que pueden ser múltiplos de 7 constituyen un conjunto unitario que demuestra la reproducción áurea oculta en estas reproducciones. Estas sumas posibles serán 14, 21, 35 y 42, dejando al 49 separado por una razón que se explicará en el punto siguiente.

Este conjunto de cuatro sumas se relacionan del siguiente modo:

(hipotenusa del triángulo áureo)

(b) - (a) = 0,381966011...(segmento menor de la proporción áurea)

(a) - (d) = 0,618033988... (segmento mayor de la proporción áurea)

(reproducción de (b))
 
 

c) En cuanto a la suma de guarismos 49 que pudiera resultar, se trata del cuadrado de 7, y tiene que tener una relación invertida con la clave 28:

Esta periodicidad (142857) que surge de los decimales de Pi está directamente relacionada con el círculo cromático, la tetractys de Pitágoras, y la música, entre otras cosas y permite señalar muy concretamente el misterio del hombre mediante la geometría, la matemática, la música y los colores.

Se trata de algo científico y a la vez artístico y por consiguiente estético.

Será la médula del capítulo siguiente.

Para verificar la armónica relación de esta periodicidad en los decimales de Pi con lo descrito en los capítulos anteriores, se toman los primeros 13 fragmentos de siete decimales según los obtiene el sistema matemático en uso:
 
 
 

    En el primer fragmento, además de la sumatoria 28, sucede que la multiplicación de sus decimales arroja el siguiente resultado:

1 * 4 * 1 * 5 * 9 * 2 * 6 = 2160

Se trata de un resultado que tiene una relación matemática directa con la recurrencia circular que se está poniendo de manifiesto, ya que multiplicado por 12 es igual a 25920, es decir la cantidad de años del círculo de precesión de los equinoccios.

De modo que los 12 primeros fragmentos considerados no sólo representan las 12 divisiones de 30 grados del ciclo de precesión sino que además representan cada uno de los 12 pasos o movimientos del triángulo áureo constituyendo un círculo recurrente en las 28 casillas del perímetro del cuadrado de 8, tal como ya se ha comentado.

Y el último fragmento, el 13, está tomado para indicar la posibilidad de quebrar esa recurrencia áurea pasándola a otro círculo potenciado o elevado.

Esta serie de fragmentos de siete decimales queda visualizada en el siguiente cuadro:
 
 

Lo que primeramente se observa es que en el subtotal de los 12 primeros fragmentos los números 12 y 78 están íntimamente relacionados por que 78 es precisamente la sumatoria de 12, y si ambos números son multiplicados entre sí el resultado es 936 (los números faltantes 369, en la recurrencia periódica, que se encuentran expresados de un modo invertido).

Este resultado 936 no es algo arbitrariamente desprendido y sin contacto con esta tabla, porque dividiéndolo por 28 (la clave de la tabla) arroja el siguiente resultado:

Un resultado cuyos decimales periódicos coinciden exactamente con los decimales de la suma total 4,428571 428571...

Y por otro lado el entero 33 multiplicado por 28 conduce a los 924 mts. del perímetro del cuadrado de la base de Keops que todos los investigadores reconocen como circular porque han detectado el factor Pi en las proporciones de la Gran Pirámide.

Surge algo notable si se obtiene la diferencia entre el número 936 con el 369 faltante en la periodicidad:

936 - 369 = 567

El resultado es la suma de las medidas en metros y exteriores de Keops:

147 mts. altura.

189 mts. arista.

567 total.

Demasiada coincidencia para negar rotundamente la presencia de una intencionalidad en la construcción y el conocimiento desde el cual fue realizada.

Esas tres medidas son múltiplas de 7, y tienen el número periódico como puente entre sus relaciones:

Es también una extrema "coincidencia" que el matemático griego Arquímedes le diera a Pi el valor de , es decir 3,142857 142857 142857...

En 1882 el matemático alemán Ferdinand Lindemann demostró que "Pi" es un número trascendente, esto es, no puede ser la raíz de una ecuación polinómica con coeficientes racionales, y de esta manera llegó a demostrar la imposibilidad de la cuadratura del círculo, pero no fue absoluto y lo condicionó específicamente agregándole "mediante álgebra o usando la regla y el compás". De modo tal que no afirmó que fuera de estas condiciones específicas la cuadratura del círculo resultara posible.

Esta puerta abierta, que dejó el matemático alemán, es una demostración de que "matemáticas es el estudio de las relaciones entre cantidades, magnitudes y propiedades, y de las operaciones lógicas utilizadas para deducir cantidades, magnitudes y propiedades desconocidas" (Enciclopedia Encarta 2000) y se agrega: "hacia mediados del siglo XIX las matemáticas se empezaron a considerar como la ciencia de las relaciones, o como la ciencia que produce condiciones necesarias".

Regresando ahora a los fragmentos de 7 decimales de Pi, en estos 13 fragmentos aparece el número 28 en dos oportunidades que dividido por sí mismo, siguiendo el sistema del procedimiento propuesto, arroja como resultado la unidad. Y además la recurrencia periódica consta de 6 dígitos. ¿Podría este hecho conducir matemáticamente a un Pi de 6 dígitos?

He aquí la fórmula:

3,14159...=2 * 

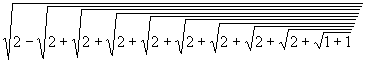
La multiplicación por 2 a la potencia 10 se debe a la cantidad de radicalizaciones sucesivas, es decir diez.

¿Y podrían ahora estos hechos matemáticos conducir a la proporción áurea?

La fórmula es la siguiente:

1,618033988...=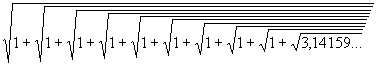

Aprovechando los condicionamientos que indicó el matemático alemán Ferdinand Lindemann y saliéndonos de los mismos, la cuadratura del círculo es posible.

La demostración geométrica de la cuadratura del círculo ahora es posible obteniendo la siguiente recta:

que geométricamente se obtiene del siguiente modo:

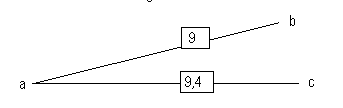
Se divide la recta "ab" en 9 partes iguales. Luego se une el punto "b" con el punto "c":

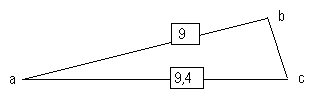
Seguidamente desde los 8 puntos divisorios dentro de la recta "ab" se trazan paralelas a la recta "bc", de modo tal que cada uno de los 9 fragmentos que se producen en la recta "ac" miden 1,0444444...

Practicando geométrica la división áurea sobre esta recta con un triángulo cuyos catetos sean 1,0444444... y su mitad, el segmento áureo menor mide:

Ahora se construye un cuadrado con lado (d) y se traza su diagonal:

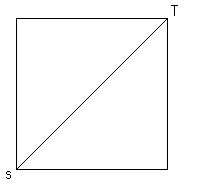
La diagonal ST mide:

Finalmente y con la recta (e) como radio se traza un círculo cuya área será:

Es decir UNO hasta 8 dígitos UNICAMENTE, con lo cual se cuadra el área de un círculo con un cuadrado de lado uno mediante un factor Pi de 8 dígitos: 3,1415926, es decir con siete decimales.

De modo tal que el área 1 del círculo queda cuadrada con el área de un cuadrado de 1 por lado.

No se trata de una cuadratura del círculo obtenida "mediante álgebra o usando la regla y el compás", sino utilizando matemáticas de un modo complementario con la geometría, sin necesidad de estar midiendo a farolazos limpios con la regla y el compás.

Y se llega a este resultado con un círculo de área UNO que se cuadra con el área de un cuadrado cuyos lados miden la unidad.

Las razones por las cuales el Pi que origina esta cuadratura es de siete decimales y sin aproximación alguna sino con precisión científica (sin fragmentar a las matemáticas de las diferentes disciplinas científicas), surgirán al completar el desarrollo del significado de la cuadratura.

 la antigüedad y en la actualidad un matemático es un sabio, no un especialista.
( Tomado de �Teoremas de la existencia humana�, de Abelardo Falletti, edición 1999, ISBN 987-043-0217-8 )
volver