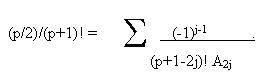
Alberto Espinoza Castillo
Lima- Perú
11.Mayo.2001
Las infinitas cifras de pi, finalmente, pueden tener todas las combinaciones que queramos. Quizás hasta se repita una cantidad apreciable de las mismísimas cifras de pi, dentro del mismo pi, una o varias veces, como de casualidad, en algún lugar muy lejano, distante a millones de años luz de la coma decimal... sin que podamos demostrarlo, por ahora... por lo que deberíamos guardar nuestro asombro para cuando esto ocurra...
Lo que sí asombra ahora es la relación de hermandad entre pi y los números primos, como esta:
(1-1/22)(1-1/32)(1-1/52)(1-1/72)(1-1/112)(1-1/132) .... = 6/p2 ........ (a)
... aunque obviamente es más hermosa la generalización de la relación entre la potencia p de pi, y las p-potencias de los números primos:
(1-1/2p)(1-1/3p)(1-1/5p)(1-1/7p)(1-1/11p)(1-1/13p) .... = Ap / pp ........ (b)
en donde se pueda determinar el valor de Ap (número racional), como función de p.
Para encontrar el vínculo general entre los números primos y pi con pocas herramientas matemáticas, no nos queda más que la intuición y el aprovechamiento de las analogías ... y tener fe en que las leyes matemáticas deben ser sencillas y bellas, a diferencia de las otras leyes que algunos las respetan solo a regañadientes...
Veamos. Recordemos que existe una fórmula que permite obtener pi, utilizando la sumatoria de las inversas de los cuadrados de los números enteros:
1/12 + 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + .... = p2/6 ........ (c)
¡Ajá!... comparando las expresiones (a) y (c) ya se están dando cuenta de algo...
Bueno, sigamos:
Para las cuartas potencias:
1/14 + 1/24 + 1/34 + 1/44 + 1/54 + 1/64 + .... = p4/90 ........ (d)
(Por si acaso, Euler obtuvo las expresiones c y d)
Para las sextas potencias:
1/16 + 1/26 + 1/36 + 1/46 + 1/56 + 1/66 + .... = p6/945 ........ (e)
Para las octavas potencias:
1/18 + 1/28 + 1/38 + 1/48 + 1/58 + 1/68 + .... = p8/9450 ........ (f)
La cosa se pone fácil. Si analizamos los denominadores de estas expresiones: 90, 945, 9450... notamos hábilmente que el número 945 se obtiene multiplicando por 10.5 el 90, y que 9450 se obtiene multiplicando por 10.0 el 945.... por lo que inducimos que el siguiente número de la serie tiene que ser: 9450 por 9.5, osea: 89775.... y así de fácil, obtenemos la fórmula que relaciona a pi con las décimas potencias de los números enteros:
1/110 + 1/210 + 1/310 + 1/410 + 1/510 + 1/610 + .... = p10/89775 ........ (g’)
Desgraciadamente no podemos gritar ¡eureka!. Si calculamos pi con esta fórmula, su valor sería 3.128662478298... La verdadera fórmula que relaciona a pi con las décimas potencias de los números enteros es:
1/110 + 1/210 + 1/310 + 1/410 + 1/510 + 1/610 + .... = p10/93555 ........ (g)
Con lo visto hasta el momento, podemos afirmar fehacientemente que el denominador del valor derecho de la fórmula para las duodécimas potencias es un número entero... equivocándonos nuevamente, dado que:
1/112 + 1/212 + 1/312 + 1/412 + 1/512 + 1/612 + .... = p12/ (638 512 875 / 691) ........ (h)
Lo que sí podemos decir, a estas alturas, es que existe una fórmula general para:
1/1p+ 1/2p + 1/3p + 1/4p + 1/5p + 1/6p + .... = pp/A(p) ........ (i)
Podemos calcular el valor de A(p) en función de los valores A2, A4, .... , A(p-2) utilizando la fórmula (j):
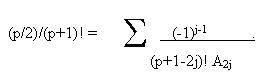
Nota: Para ser sincero, primero uno se da cuenta que las series de Euler para pi pueden extenderse para otras potencias pares (o impares... pero para nuestros propósitos, solo vamos a considerar las potencias pares.... ya verán porqué...), y generalizar luego para cualquier potencia par "p", observando los valores de "A" respectivos que van saliendo a medida que calculamos la sumatoria y la relacionamos con el "verdadero" valor de la potencia p de pi.
Mediante la fórmula (j), se halla, para p=14, que :
7/15! = 1/ (13! * A2) - 1/ (11! * A4) + 1/ (9!
* A6) - 1/ (7! * A8) + 1/ (5! * A10)
- 1/ (3! * A12) + 1/ (1! * A14)
.... (k)
Pero, sabemos que: A2 = 6, A4 = 90, A6 = 945, A8 = 9450, A10 = 93555,
A12 =638 512 875 / 691
Entonces, reemplazando estos valores en (k), tenemos que: A14 = 9 121 612.5; y :
1/114 + 1/214 + 1/314 + 1/414 + 1/514 + 1/614 + .... = p14/ (9 121 612.5) ........ (l)
con la que solamente considerando el primer término de la serie infinita, se calcula para pi un valor de 3.14157891, y con los dos primeros términos, 3.141592606....
Con las fórmulas (i) y (j), podemos encontrar la fórmula para obtener pi para cualquier potencia par.
Pero, al empezar este estudio dije que determinaríamos la relación que existe entre la potencia p de pi, y las p-potencias de los números primos:
Experimentemos. Sea:
(1-1/2p)(1-1/3p)(1-1/5p)(1-1/7p)(1-1/11p)(1-1/13p) .... = k ........ (m)
Para p=6, y usando "todos" los números primos (bueno... "bastantes"), el valor de k resulta ser: 0.982952592265.
Ahora, suponiendo que la fórmula (b) fuera cierta, tenemos que:
A6 = k p6 = 945, que "coincide" con el acompañante de p6 de la fórmula (e).
Del mismo modo, para p=8, se obtiene: k=0.995939201125
Entonces: A8 = k p8 = 9450 ... Notemos la "coincidencia" con (f)
Para p=10, k=0.999006413069
Entonces: A10 = k p10 = 93555 ... Notemos esta nueva "coincidencia", con (g)
Para p=12, k=0.999753973990
Entonces: A12 = k p12 = 924041.787264823 ó 638 512 875 / 691 ...Pero, ¡estamos con suerte! Comparemos este valor con el de la expresión (h)... ¿es tan ordenado el azar?
... Pero ¡basta ya de coincidencias! ... Hay un proverbio chino que dice: Si un hombre te dice caballo, ríete de él... Si un segundo hombre te dice caballo, duda... Si un tercer hombre te dice caballo... anda pensando seriamente en comprarte montura y herraduras...y podría agregarse que si un cuarto hombre de dice caballo, relincha nomás...
Ahora sí, con plena certeza podemos apostar que para p=14, A14 = 9 121 612.5, tal y como se obtuvo en la expresión (l)
Finalmente, la relación entre la potencia p (número par) de pi, y las p-potencias de los números primos, es ésta:
(1-1/2p)(1-1/3p)(1-1/5p)(1-1/7p)(1-1/11p)(1-1/13p) .... = A p / pp
Siendo (según la fórmula (j) ):
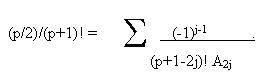
Ejemplos:
(1-1/22)(1-1/32)(1-1/52)(1-1/72)(1-1/112)(1-1/132) .... = 6 / p2
(1-1/24)(1-1/34)(1-1/54)(1-1/74)(1-1/114)(1-1/134) .... = 90 / p4
(1-1/26)(1-1/36)(1-1/56)(1-1/76)(1-1/116)(1-1/136) .... = 945 / p6
(1-1/28)(1-1/38)(1-1/58)(1-1/78)(1-1/118)(1-1/138) .... = 9450 / p8
(1-1/210)(1-1/310)(1-1/510)(1-1/710)(1-1/1110)(1-1/1310) .... = 93 555 / p10
(1-1/212)(1-1/312)(1-1/512)(1-1/712)(1-1/1112)(1-1/1312) .... = (638 512 875 / 691)/ p12
(1-1/214)(1-1/314)(1-1/514)(1-1/714)(1-1/1114)(1-1/1314) .... = 9 121 612.5 / p14
y así, sucesivamente, podemos generar todas las fórmulas que queramos para cualquier potencia par "p", en la que el valor de la potencia "p" de pi, se relaciona con las potencias "p" de los números primos...¿No asombra tanta belleza?...