"Este trabajo está dedicado a mi profesor de quinto de primaria ( el profesor Medina) quien tomó el único balón de baloncesto de la escuela pública Juan Manuel Rudas, en Honda (Tolima), y con una tiza blanca trazó sobre éste el círculo máximo y dijo: �Y con ésto empieza la historia de pi... el resto no tiene cuando acabar..." (1964)

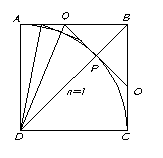
En el siguiente trabajo presentaré un nuevo algoritmo, que he desarrollado, para el cálculo del número PI (p ) utilizando el siguiente procedimiento: se toma un cuadrado de lado 1 (unidad) y sobre éste se superpone la cuarta parte de un círculo cuyo radio es igual al lado del cuadrado, ver figura #1; ahora se procede a realizar cortes de los sobrantes del cuadrado tal como lo represento en la figura #2

Figura #1

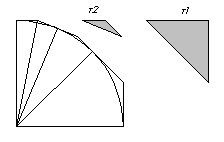Figura #2

La idea es ir quitando estos triángulos hasta aproximar, con los cortes, el cuadrado a una circunferencia, en este caso a la cuarta parte.

Se ve en la figura #1 que el primer triángulo es el formado por los puntos QBO, de éste tendríamos cuatro en total si tuviéramos un círculo completo, luego se recorta el triángulo T2 (figura #2) de los cuales tendríamos dos en este cuadrante para un total de ocho triángulos T2; este procedimiento lo podríamos continuar -en forma interminable- hasta lograr que el cuadrado recortado se aproxime lo mejor posible al borde de la cuarta parte del círculo dado.

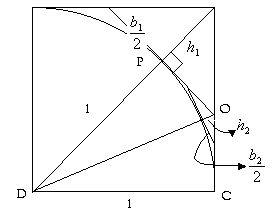
En la figura #3 representa la altura del primer triángulo recortado T1 y la base como cuyo valor medio es , podemos deducir que , ahora el valor de la altura será: , en el triángulo T2 tenemos, de forma análoga, que su altura es y su semi-base sería ; la relación entre los triángulos DPO y la mitad del triángulo T2 está dada por la siguiente ecuación: ; como el triángulo DPO es rectángulo, se logra obtener la ecuación:

Que al simplificar y reemplazar los b en función de los h, nos quedaría: , cuya solución en daría: ; si realizamos el mismo procedimiento para se llega a esta otra ecuación: 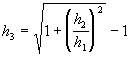; para continuar hasta llegar a la ecuación siguiente de las n diferentes alturas: .

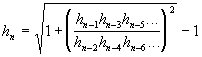Ahora se calculará el área de cada triángulo de tal manera que se pueda decir que cada vez que se quita, con un corte, un grupo de triángulos entonces nos aproximamos al área del círculo.

El área del primer triángulo es ; que reemplazando la base en función de la altura, nuestra área se convertirá en: ; si continuamos con la siguiente área llegamos a ; y si así continuamos con el resto de las áreas llegaremos a la ecuación: ; que se puede transformar en: 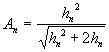; utilizando la ecuación �recurrente� anterior para calcular las alturas de cada triángulo, ésta última ecuación nos simplifica los algoritmos para realizar cálculos repetitivos en computador.

El área total del cuadrado es de 4 si solamente representamos, en la figura #1, a un solo cuadrante, el área del círculo completo es de p (1)² con lo cual tendríamos la ecuación para el cálculo final así:

En forma de sumatoria se puede escribir:

También podemos decir que PI, como función de las alturas enésimas, tendría una ecuación de la siguiente manera:

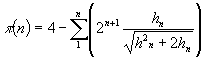
Que sería igual a PI si n tiende a infinito. Realizaremos algunos cálculos para verificar nuestra ecuación y observar cómo nos aproximamos, poco a poco al número PI.

De la tabla anterior se observa que son necesarias más iteraciones para lograr un acercamiento al verdadero valor de PI, o sea que entre más cortes se logren más aproximado es el algoritmo al valor real de PI.

Se realizó un cálculo utilizando el programa Maple V, con 1300 iteraciones y 650 decimales y se observa en los dos cálculos abajo, el TPI2 es calculado con el algoritmo, y el otro es tomado de un libro, se puede observar que la diferencia está al final, ( favor buscar) en las cifras 0513200338... y en el de base aparece 051320005681... ésto nos indica que es necesario continuar con más iteraciones y luego se volvería a presentar otra diferencia. Etc..., y entre más se itere mejor es la precisión.

Por lo tanto el algoritmo converge hacia PI.

�Porqué elaborar algoritmos para PI? Desde el punto de vista práctico el problema está resuelto, basta tomar algunos instrumentos de muy buena precisión y realizar unas medidas y estaremos cerca de 3,141592 pero tal vez no más (sería costoso) Luego solo nos queda la parte analítica para penetrar en la naturaleza, extensión y trascendencia de un número. Lo sorprendente de PI es que podemos llegar a él por medios tan distintos que lo hacen fascinante. Son muchos los algoritmos que existen. En el caso del algoritmo que presento si se hace el procedimiento con un cubo para llegar a una esfera de radio unidad; también tendríamos otra forma de llegar a PI.

Veamos algunos algoritmos desarrollados ─ya en su fórmula final─:

POR ARQUIMEDES:

**********************************************************************

POR FRANCOIS VIETE:

**********************************************************************

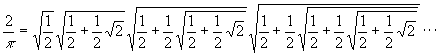
POR JOHN WALLIS

**********************************************************************

POR ISAAC NEWTON

**********************************************************************

POR GOTTFRIED LEIBNITZ

**********************************************************************

POR LEONARD EULER

�����������������������������������

**********************************************************************

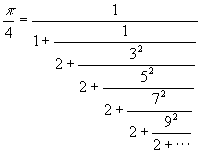
POR SHANKS

**********************************************************************

POR BROUNCKER

**********************************************************************

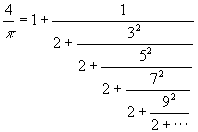
POR RAMANUJAN

, , ,

���������������������������������.��

**********************************************************************

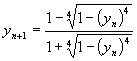POR MACHIN

**********************************************************************

POR FERNANDO VALDES

, ,

,

�����������������������������������

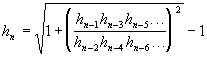
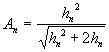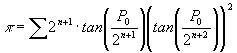
(enfoque trigonométrico)

**********************************************************************

Aunque no soy muy amigo de las fórmulas trigonométricas para estos algoritmos porque éllas conllevan una serie matemática u otro algoritmo en forma implícita, he querido también presentar una ecuación con enfoque de trigonometría, que acompaña la lista anterior a la ecuación algebraica, que se puede deducir de las gráficas que he utilizado en la parte inicial de este documento.

Decía, al comienzo, que he cortado las puntas, en el dibujo, para llagar al círculo; me llamó la atención los pedacitos que sobran de este proceso: obtuve una figura con "todos" estos sobrantes y la llamé: "El amanecer de PI, o sol de PI" favor ver la figura # 4.

Figura # 4

Beckmann, Petr., a history of PI, St. Martin�s Press, New York